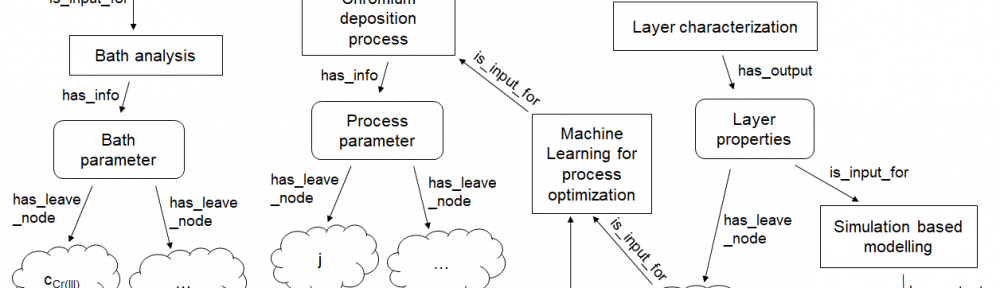
In order to make material design processes more efficient in the future, the underlying multidimensional process parameter spaces must be systematically explored using digitalisation techniques such as machine learning (ML) and digital simulation. In this paper we shortly review essential concepts for the digitalisation of electrodeposition processes with a special focus on chromium plating from trivalent electrolytes.

Introduction

Electrodeposition is a powerful technique to give the surface of materials special properties. Depending on the application the electrodeposited coating must have specific physical and chemical properties. For example, a hard chromium layer usually should have a minimum thickness of several microns with optimized tribological properties, whereas a bright chromium layer should be relatively thin with a special visual appearance. It is well known that one can tune the properties of electrodeposits via the process parameters. However, depending on the complexity of the system, it may take a long time to find the optimal process parameters if one resorts to trial-and-error approaches. In order to minimize the time for optimization, computer guided research strategies can be applied. This paper presents the authors’ viewpoints on how a digitalisation approach can be used to better understand relationships between the process parameters and the properties of electrodeposited coatings. The columns on which such a digital approach will rest are machine learning, ontologies, and digital simulation. The discussion is focused on electrodeposition from trivalent chromium baths, as this system has a high technical relevance and at the same time is characterized by a high physicochemical complexity.

Machine learning

The principle of machine learning (ML) is based on algorithms that independently recognize and learn from correlations between input and output data, so that the correlation data obtained significantly reduce the effort of testing methods for quality assurance in an industrial process. The usage of ML algorithms for scientific discovery is a popular recent trend, especially in conjunction with Explainable AI (XAI) [1]. After training a ML model, scientific knowledge is gained by either explaining the model or the predicted output. Key components are design- and algorithmic transparency, model- and output interpretability as well as the integration of domain knowledge [1]. An important advancement especially in ML-driven material science is the usage of deep learning, as it eliminates the manual feature engineering step of classical ML approaches. This reduces barriers in the application of ML in material discovery and design [2]. Among deep learning, Convolutional Neural Networks (CNNs) are one of the enabling key technologies [3–6]. They are specifically designed for data in the form of multiple arrays, e. g. images, spectrograms or volumetric images [7]. The usage of local connections and shared weights in the form of convolution layers as well as the pooling operation allows using many layers. Those layers then extract hierarchical patterns [7]. One XAI technology that is regularly used in conjunction with CNNs is Grad-CAM [8]. It generates a heatmap highlighting prediction-relevant areas of the images, which is used for output interpretability.

So far, ML has not been used extensively and only in a rather rudimentary form in electroplating. Here, we review the main approaches reported to date. Leung et al. emphasize the need of modern competitive companies using electroplating processes to capture and reuse tactics and explicit knowledge in times of “brain drain”. As there is always a natural loss of knowledge which accompanies the loss of experienced staff members, any countermeasures such as the use of on-line analytical processing (OLAP) and fuzzy logic approaches [9].

Furthermore, the concepts of rule based and case based reasoning were used to simplify the decision processes involved in electroplating, making use of different degrees of objective- and subjectiveness. The latter allows experts to rewrite rules and further improve the outcome of the somewhat automated reasoning. The general goal is to reduce response times by addressing problems in the electroplating process itself in a defined and reproducible way. These tools can furthermore be applied to accurately price the plated substrates, which is especially important in the field of noble metal plating [10].

Artificial neural networks (ANNs) have been applied and compared to regression models for the prediction of the plating efficiency in alloy deposition, using alkaline cyanide copper tin electrolytes. Due to the presence of complex nonlinearities, which are in general characteristic for electroplating, ANNs were shown to be superior on classical linear and exponential regression models [11].

Rashidi et al. [12] and Hayati et al. [13] compared the use of an adaptive neuro-fuzzy inference system (ANFIS) with such kinds of ANNs in the prediction of grain size in nanocrystalline nickel coatings deposited from a Watts type nickel electrolyte as a function of current density, saccharin concentration and electrolyte temperature, proofing a higher accuracy of the ANFIS.

Also, ANNs were used to predict the wear properties of electroplated hard chromium layers by correlating the friction moment to wear test parameters [14, 15].

Paatsch et al. used ANNs to develop operating maps to model the relationships between plating parameters (electrode potential, metal content, current off-time, duty cycle, electrolyte convection), process characteristics (current-potential relation, current efficiency) and functional layer characteristics (textures, layer hardness, Young´s modulus, creep parameter, all relating to layer microstructure, ductility and finally mechanical layer performance), in the field of pulse plating from alkaline Zn electrolytes [16].

Furthermore, machine learning methods (neural networks in a multilayer perceptron (MLP), using error backpropagation (EBR), polynomial regression (PR), support vector regression (SVR), extreme learning machine (ELM), fully connected cascade (FCC) using a neuron-by-neuron (NbN) algorithm) were used to predict the additive concentration (accelerator, suppressor and leveller) in unknown plating bath samples used for vias in semiconductor plating and electronics packaging [17].

In another paper, the thickness of hard chromium layers, an intrinsically critical issue thereof, could be precisely predicted by the use of evolutionary support vector machines (ESVMs). Achieving a homogeneous hard chromium layer thickness distribution is hampered by the intrinsically negative throwing power of hard chromium electrolytes. Therefore, a multistep process is being applied, which also defines the input parameters such as chromium acid content in the hard chromium electrolyte, electrolyte temperature, plating time, electropolishing temperature and time, iron content in the electropolishing electrolyte and thickness removed by electropolishing [18, 19].

Mathematical models are also used to explain why keeping the temperature of a chromium plating bath constant is important in industrial applications, and what can happen in terms of qualities of deposited films, if this is not the case [20].

Different ML methods were used to identify which additives can be used as corrosion inhibitors for aluminium alloys that are used in aerospace applications [21]. The pH of the solution as well as the type of the alloys were included in the model as variables, and used together with the art of the inhibitor to train the algorithm.

Ontologies

The application of ML techniques to large parameter spaces is closely related to the task of structuring the information of these spaces to make them processable by digital algorithms. Data sets must be combined in such a way that the data can be processed by computer algorithms. This is where ontologies come into play. By definition an ontology is a formal explicit specification of a shared conceptualization. Ontologies allow the modelling of complicated knowledge concepts. An important concept is the triple subject – predicate – object, e. g. “electroplated layer” “is a” “material”. Usually ontology modelling is a multi- step iterative process. Therefore, the first step for using ML in electroplating is to build an ontology for electroplating. This ontology should describe the electroplating process and the properties of the resulting products, in this case electroplated layers (Fig. 1). Once this framework is set up it can be fed with data. The data can come from experiments and from digital simulations. The latter is an attractive option if experimental data cannot be obtained easily. An example could be elastic properties of thin layers.

Fig. 1: Example of an ontology for the description of the electrodeposition of chromium and the characterization of the layer properties. The scheme contains optimization loops for the chromium deposition process by ML and simulation based modelling

Digital procedures for electroplating based on ontologies seem to be scarce in literature. There are several reasons for that. On the one hand, electroplating processes are usually very complex and characterised by many, mostly interdependent variables of the chemical and physical process parameters. Therefore, they should be predestined for the use of such methods, but on the other hand, the high complexity is at least a psychological hurdle. Some interactions, e. g. caused by degradation products of organic additives, have not yet been fundamentally researched, which often results in empirical control strategies for electroplating processes, such as the dosing of ready-made solutions to the plating bath after a certain electrical charge has been passed or disposing and replenishing part of the bath. Of course there is no denying the fact that these approaches may work very well. However, this complexity and partly unknown interactions should not be an excuse or even an obstacle for the use of digital methods, but rather a logical necessity to use such tools in complex electrochemical surface treatment. This necessity naturally increases with the use of increasingly complex high-performance electrolytes and the demand for ever lower reject rates.

Digital simulation for material research

Micro- and nano-indentation testing is frequently used for the mechanical characterization of thin films. Besides the hardness of the film, the indentation modulus can be obtained from instrumented indentation testing such as Figure 2.

Fig. 2: Instrumented indentation test of a chromium layer deposited from 0.5 M choline chloride, 1 M ethylene glycol with 0.5 M CrCl3*6H2O at 80 °C. Maximum force applied was 25 mN and it was a 5 s delay between the loading and the unloading curves

For thicknesses above 1 µm the hardness of layers can be easily determined experimentally. However, it is challenging to determine the hardness of thin layers as the measured indentation curve will be a convolution of several parameters, e. g. the properties of the substrate and the shape of the indenter. In this case, digital simulation can be the method of choice to predict the mechanical properties of thin deposits. Based on results of finite-element simulations of indentation tests in film-substrate systems, critical ratios for the indentation depth to film thickness could be derived. This is a useful guide to ensure a negligible effect of the substrate properties. Further more, analytical functions that describe the hardness-indentation depth relation were established, e.g. [22–27].

The effect of residual stresses on hardness, e. g. [28, 29], as well as of imperfections of the indenter (usually present for micro- and nano- indentation testing), e. g. [30, 31], was estimated in finite-element simulations. From comparisons of simulated results with experimental results, the continuum based finite-element simulation shows the capability to determine the load-indentation depth response even of sub-micrometer indentation testing [32].

Hence, using finite element simulations of indentation tests, further insights can be gained to complement experimental results, allowing a more reliable evaluation of mechanical properties and their sensitivities.

However, hardness and indentation modulus describe the mechanical properties of the film quite superficially, especially if the film can undergo plastic deformation. The same hardness can be obtained for elastic-plastic materials with different stress-strain curves (e. g. lower initial yield stress with pronounced strain hardening and higher yield stress with low strain hardening) [33].

Hence, methods have been proposed to derive the full stress-strain curve from results of indentation tests using finite-element simulations. With sharp indenters, the stress-strain curve can, however, not be obtained uniquely from load-indentation depth curves so that usually results obtained with different sharp indenter geometries are used [34, 35].

In contrast to sharp indenters, spherical indenters do not generate a load-independent characteristic strain so that the elastic-plastic properties are continuously represented in the load-indentation depth curve and the stress-strain curve of thin films and bulk materials can be determined from spherical indentation tests, e. g. [36, 37].

From cyclic spherical indentation tests, even hardening properties of the material related to cyclic loadings can be derived. In particular, from a cyclic load-indentation depth curve showing a hysteresis loop during unloading and reloading, material properties of isotropic and kinematic hardening laws can be determined and the cyclic stress-strain curve is obtained [38–40].

With such material properties known for thin films, a more detailed analysis of the mechanical behavior of thin films regarding lifetime limiting mechanisms as e. g. cyclic wear or cyclic substrate deformations is possible. Moreover, based on process-properties relations the deposition and chemical composition of films could be optimized with respect to the actual lifetime limiting loading condition.

The microstructure of thin films and bulk materials have a significant effect on their properties. Using microstructure-based finite-element simulations, in which the microstructure of the material (as e. g. the polycrystalline structure of a hard chrome plating) is explicitly resolved, microstructure-property relations can be assessed in computer experiments with a high number of microstructure variations. For example, the effect of grain shape, grain orientation and the misorientation of grains (i. e. the grain boundary type) as well as their statistical distributions on the mechanical properties of a film or bulk material can be investigated, e.g. [41, 42].

Furthermore, the effect of the spatial distribution, the size distribution and the volume fraction of inclusions, as e. g. particles in dispersion coatings, can be assessed with respect to macroscopic properties as well as local stress and strain distributions and interface tractions, e. g. [43–45].

The material properties of single grains or phases can, again, be derived from indentation testing in combination with finite-element simulations [46–51].

The combination of indentation testing and finite-element simulation, hence, allows more meaningful material properties of a thin film to be determined with respect to the lifetime limiting loading conditions. From the microstructure-based assessment of thin films and the feedback of the results back into the process control, improved load-adapted coatings can be developed. To this end, an ontology for thin films is required to systematically address process-microstructure-properties correlations combining experimental data and simulation data.

Application of digital material research to electrodeposition of chromium

In the following we will discuss as an example the highly relevant material system of electroplated chromium layers based on trivalent chromium electrolytes. Due to REACh-driven regulations it is particularly predestined to be investigated by digitalisation techniques. On the one hand, it offers a large parameter space. On the other hand, it is characterized by a broad industrial application spectrum in the decorative as well as in the functional field. The industrial requirements for chromium coatings from trivalent baths must ideally result in the same coating profile as coatings made from hexavalent chromium electrolytes or excel them. In addition to the reduction of health risks for the user, there could be further advantages in terms of increased energy efficiency through increased current efficiency, lower hydrogen evolution.

Microstructure, surface morphology and chemical composition of the electroplated chromium strongly depends on the type of electrolyte used. Hexavalent chromium electrolytes offer a nano-sized grain structure and a low amount of impurities. The deposit exhibits high hardness (around 1000 HV_0,1), good abrasive and sliding behaviour and a resistance against corrosion in aqueous media. A high brightness and blueish colour hue is achieved for decorative applications. As the bath composition is relatively simple and the sensitivity against organic and metallic contaminants is very low, the layer properties are easy to maintain in industrial processes.

Compared to the hexavalent baths the compositions of trivalent chromium electrolytes are much more complex. Chromium(III) forms a kinetically inert aqua complex, so that the reduction to metallic chromium is hindered and additives are needed to facilitate the reduction process, e.g. carboxylic acids as complexing agents [52, and refs. within]. Other organic compounds are added in order to improve coverage, throwing power or microstructure of the coating. The incorporation of carbon caused by the decomposition of these additives can have a beneficial effect on the hardness and the visual appearance of the deposits. However, the deposition of thick chromium layers from trivalent electrolytes is challenging as high internal stress and crack formation may occur. Since microstructure and layer composition differ from hexavalent chromium based processes, the corrosion resistance is often not sufficient, and the optical appearance does not meet the requirements for decorative applications. Furthermore, trivalent chromium electrolytes are far more sensitive against process fluctuations and contaminants due to drag-out from other process solutions.

Cr(III) is a comparatively highly complex electrolytic system and diametrically opposed to Cr(VI), so that for the design and especially the mimic of conventional chromium coatings from Cr(VI) processes ML approaches can bring a high added value; in this context it is also very attractive to use the performance of structure-revealing ML processes to further develop structure-properties relations. Especially in the development of thick functional chromium layers, ML can even be a key point for the industrialization of these more environmentally friendly processes due to the high complexity of the Cr (III) processes.

Summary and Outlook

In this paper we tried to give a short review on machine learning approaches and their current use in electrochemical processes. There are still many more fields where ML methods can be successfully employed, such as to predict the roughness of metallurgical powders that can be used in dispersion coatings for example. Although some reports based on ML methods can be already found in the literature, there is still much work to be done in order to understand the relationship between the electroplating process parameters and the properties of the deposits. As ML algorithms must be fed with high quality data, we also discussed digital simulation as an additional data source besides experiments. And finally the data space of data must be structured using an ontology in a manner that at the same time ML and human beings can make the best use of it.

In summary, we think that the future of sustainable electroplating surely lies with computer assisted research.

References

1. R. Roscher; B. Bohn; M.F. Duarte; J. Garcke: Explainable Machine Learning for Scientific Insights and Discoveries, IEEE Access 8 (2020) 42200–42216
2. J. Cai; X. Chu; K. Xu; H. Li; J. Wei: Machine learning-driven new material discovery, Nanoscale Advances 2 (2020) 3115–3130
3. K. Simonyan; A. Zisserman: Very Deep Convolutional Networks for Large-Scale Image Recognition, International Conference on Learning Representations (ICLR), 2015
4. K. He; X. Zhang; S. Ren; J. Sun: Deep Residual Learning for Image Recognition, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2016) 770–778
5. F. Chollet: Xception: Deep Learning with Depthwise Separable Convolutions. IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2017) 1800–1807
6. M. Tan; Q.V. Le: EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks, Proceedings of the 36th International Conference on Machine Learning (2019)
7. Y. LeCun; Y. Bengio; G. Hinton: Deep learning, Nature 521 (2015) 436–444
8. R.R. Selvaraju; M. Cogswell; A. Das; R. Vedantam; D. Parikh; D. Batra: Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization, Proceedings of the IEEE International Conference on Computer Vision (ICCV) (2017) 618–626
9. R.W.K. Leung; H.C.W. Lau; C.K. Kwong: An Intelligent System to Monitor the Chemical Concentration of Electroplating Process: An Integrated OLAP and Fuzzy Logic Approach, Artificial Intelligence Review 21 (2004) 139-159
10. F.T.S. Chan: Application of a hybrid case-based reasoning approach in electroplating industry, Expert Systems with Applications 29 (2005) 121-130
11. K.Subramanian; V.M. Periasamy; M. Pushpavanam; K. Ramasamy: Prediction of cathode efficiency in electro-deposition of copper-tin using regression and artificial neural network model, Journal of Electroanalytical Chemistry 648 ( 2010) 176-183
12. A.M. Rashid;, A.R. Eivani; A. Amadeh: Application of artificial neural networks to predict the grain size of nano-crystalline nickel coatings, Computational Materials Science 45 (2009) 499–504
13. M. Hayati; A.M. Rashidi; A.Rezaei: Prediction of grain size of nanocrystalline nickel coatings using adaptive neuro-fuzzy inference system, Solid State Sciences 13 (2011) 163–167
14. T. Sahraoui; S. Guessasma; N.E. Fenineche; G. Montavon; C. Coddet: Friction and wear behaviour prediction of HVOF coatings and electroplated hard chromium using neural computation, Materials Letters 58 (2004) 654–660
15. T. Sahraoui; S. Guessasma; N.E. Fenineche: Friction moment prediction of HVOF coatings and Electroplated Hard Chromium, Materials Letters 62 (2008) 473–477
16. W. Paatsch; G. Mollath: Operating map- tool for plating functional layers, Transactions of the IMF 88 (2010) 234–236
17. C.D. Ellis; M.C. Hamilton; J.R. Nakamura; B.M. Wilamowski: Efficient Determination of Copper Electroplating Chemistry Additives, IEEE Transactions of Components, Packaging and Manufacturing Technology 4 (2014) 1380–1390
18. F. Sánchez Lasheras; P.J. García Nieto; F.J.de Cos Juez; J.A.Vilán Vilán: Evolutionary support vector regression algorithm applied to the prediction of the thickness of the chromium layer in a hard chromium plating process, Applied Mathematics and Computation 227 (2014) 164–170
19. F.Sánchez Lasheras; J.A.Vilán Vilán; P.J.García Nieto; J.J.del Coz Díaz: The use of design of experiments to improve a neural network model in order to predict the thickness of the chromium layer in a hard chromium plating process, Mathematical and Computer Modelling 52(7–8) (2010) 1169–1176
20. S. Tanthadiloke; P. Kittisupakorn; I. M.Mujtaba: Modelling and Design a Controller for Improving the Plating Performance of a Hard Chromium Electroplating Process, Computer Aided Chemical Engineering 33 (2014) 805–810
21. T.L.P. Galvão; G. Novell-Leruth; A. Kuznetsova; J. Tedim; J. R. B. Gomes: Elucidating Structure–Property Relationships in Aluminum Alloy Corrosion Inhibitors by Machine Learning, J. Phys. Chem. C 124(10) (2020) 5624–5635
22. A.K. Bhattacharya; W.D. Nix: Analysis of elastic and plastic deformation associated with indentation testing of thin films on substrates, International Journal of Solids and Structures 24 (1988) 1287–1298
23. X. Cai; H. Bangert: Hardness measurements of thin films-determining the critical ratio of depth to thickness using FEM, Thin Solid Films 264 (1995) 59–71
24. T.Y. Tsui; J. Vlassak; W.D. Nix: Indentation plastic displacement field: Part I. The case of soft films on hard substrates, Journal of Materials Research volume 14 (1999) 2196–2203
25. Y. Tsui; J. Vlassak; W.D. Nix: Indentation plastic displacement field: Part II. The case of hard films on soft substrates, Journal of Materials Research 14 (1999) 2204–2209
26. K.-D. Bouzakis; N. Michailidis; G. Skordaris: Hardness determination by means of a FEM-supported simulation of nanoindentation and applications in thin hard coatings, Surface and Coatings Technology 200 (2005) 867–871
27. Z.S. Ma; Y.C. Zhou; S.G. Long; C. Lu: On the intrinsic hardness of a metallic film/substrate system: Indentation size and substrate effects, International Journal of Plasticity
    34 (2012) 1–11
28. S. Suresh; A.E. Giannakopoulos: A new method for estimating residual stresses by instrumented sharp indentation, Acta Materialia 46 (1998) 5755–5767
29. N. Huber; J. Heerens: On the effect of a general residual stress state on indentation and hardness testing, Acta Materialia 56 (2008) 6205–6213
30. E. Tyulyukovskiy; N. Huber: Neural networks for tip correction of spherical indentation curves from bulk metals and thin metal films, Journal of the Mechanics and Physics of Solids 55 (2007) 391–418
31. J.M. Antunes; L.F. Menezes; J.V. Fernandes: Influence of Vickers tip imperfection on depth sensing indentation tests, International Journal of Solids and Structures 44 (2007) 2732–2747
32. A.K. Bhattacharya; W.D. Nix: Finite element simulation of indentation experiments, International Journal of Solids and Structures 24 (1988) 881–891
33. H. Lan; T.A. Venkatesh: On the relationships between hardness and the elastic and plastic properties of isotropic power-law hardening materials, Philosophical Magazine 94 (2014) 35–55
34. N. Chollacoop; M. Dao; S. Suresh: Depth-sensing instrumented indentation with dual sharp indenters, Acta Materialia 51 (2003) 3713–3729
35. J.L. Bucaille; S. Stauss; E. Felder; J.Michler: Determination of plastic properties of metals by instrumented indentation using different sharp indenters, Acta Materialia 51 (2003) 1663–1678
36. N. Huber; I. Tsagrakis; C. Tsakmakis: Determination of constitutive properties of thin metallic films on substrates by spherical indentation using neural networks, International Journal of Solids and Structures 37 (2000) 6499–6516
37. M. Tandler; T. Seifert; R. Mohrmann: Bestimmung von Spannungs-Dehnungskurven bei erhöhter Temperatur aus registrierenden Eindruckversuchen, Tagungsband Werkstoffprüfung 2006, M. Borsutzki, S. Geisler (Eds.), Bad Neuenahr (2006) 127–132
38. N. Huber; C. Tsakmakis: Determination of constitutive properties from spherical indentation data using neural networks. Part i: the case of pure kinematic hardening in plasticity laws, Journal of the Mechanics and Physics of Solids 47 (1999) 1569–1588
39. N. Huber; C. Tsakmakis: Determination of constitutive properties from spherical indentation data using neural networks, Part ii: plasticity with nonlinear isotropic and kinematic hardening, Journal of the Mechanics and Physics of Solids 47 (1999) 1589–1607
40. H.M. Sajjad; H. ul Hassan; M. Kuntz; B.J. Schäfer; P. Sonnweber-Ribic; A. Hartmaier: Inverse Method to Determine Fatigue Properties of Materials by Combining Cyclic Indentation and Numerical Simulation. Materials 13 (2020) 3126
41. L. Li; L. Shen; G. Proust; C.K.S. Moy; G. Ranzi: Three-dimensional crystal plasticity finite element simulation of nanoindentation on aluminium alloy 2024, Materials Science and Engineering A579 (2013) 41–49
42. A. Biswas; M.R.G. Prasad; N. Vajragupta; H. ul Hassan;
    F. Brenne; T. Niendorf; A. Hartmaier: Influence of Microstructural Features on the Strain Hardening Behavior of Additively Manufactured Metallic Components, Advances Engineering Materials 21 (2019) 1900275
43. N. Chawla; R.S. Sidhu; V.V. Ganesh: Three-dimensional visualization and microstructure-based modeling of deformation in particle-reinforced composites, Acta Materialia 54 (2006) 1541–1548
44. J. Hohe; P. Gumbsch: On the potential of tungsten–vanadium composites for high temperature application with wide-range thermal operation window, Journal of Nuclear Materials 400 (2010) 218–231
45. M. Metzger; T. Seifert: Computational assessment of the microstructure-dependent plasticity of lamellar gray cast iron – Part I: Methods and microstructure-based models, International Journal of Solids and Structures 66 (2015) 184–193
46. J. Alcalá; O. Casals; J. Ocenášek: Micromechanics of pyramidal indentation in fcc metals: Single crystal plasticity finite element analysis, Journal of the Mechanics and Physics of Solids 56 (2008) 3277–3303
47. W.B. Lee; Y.P. Chen: Simulation of micro-indentation hardness of FCC single crystals by mechanism-based strain gradient crystal plasticity, International Journal of Plasticity 26 (2010) 1527–1540
48. H. Petryk; S. Stupkiewicz; S. Kucharski: On direct estimation of hardening exponent in crystal plasticity from the spherical indentation test, International Journal of Solids and Structures 112 (2017) 209–221
49. J.K. Engels; S. Gao; W. Amin; A. Biswas; A. Kostka; N. Vajragupta; A.Hartmaier: Indentation size effects in spherical nanoindentation analyzed by experiment and non-local crystal plasticity, Materialia 3 (2018) 21–30
50. J.K. Engels; N. Vajragupta; A. Hartmaier: Parameterization of a Non-local Crystal Plasticity Model for Tempered Lath Martensite Using Nanoindentation and Inverse Method, Frontiers in Materials 6 (2019) 247
51. M. Shahmardani; N. Vajragupta; A. Hartmaier: Robust Optimization Scheme for Inverse Method for Crystal Plasticity Model Parametrization, Materials 13 (2020) 735
52. L. Büker; R. Dickbreder; R. Böttcher; S. Sadowski; A. Bund: Investigation of The Reaction Kinetics of Chromium(III) Ions with Carboxylic Acids In Aqueous Solutions and The Associated Effects on Chromium Deposition, J. Electrochem. Soc. 167(16) (2020) 162509

PDF Version of the article
[qrcode]